Rejection Sampling

Rejection sampling is a sampling algorithm to sample data from a complex multivariate distribution using a proxy distribution.

Let’s set up the scenario. Assume our target distribution \(p(x)\) is easy to sample from but only up to a normalizing constant \(Z\). So,

$$p(x) = \frac{\tilde{p}(x)}{Z}$$

where \(p(z)\) is easy to sample from. Let \(q(z)\) be any distribution that is easy to sample from. \(q(z)\) is called the proposal distribution. Define \(kq(z)\) such that it ‘blankets’ \(p(z)\) (in other words, \(kq(z) ≥ p(z))\). See Figure 1 below.

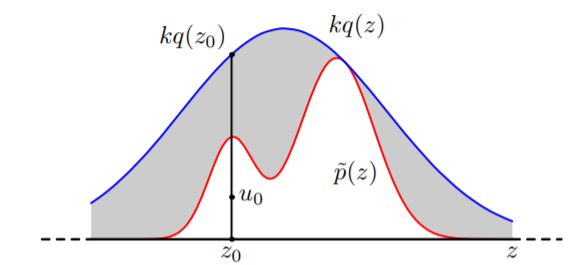
We make use of the fact that \(q(z)\) is (1) easy to sample from and (2) is never less than \(p(z).\) (1) Sampling from \(q(z)\) allows us to propose values (hence, proposal distribution) that may or may not be supported by the target distribution. (2) Because \(kq(z) ≥ p(z)\), every possible value of \(p(z)\) has a positive probability of being sampled. Therefore, we do not need to worry about missing any values.

In short, the algorithm samples some \(z_0 \sim q(z)\) and decide whether we want to accept or reject that sample based on some criteria. The resulting set of samples will be distributed according to the target distribution \(p(z).\) See Algorithm 1 for more details.