Importance Sampling

Importance sampling is an approximation method that proposes a new sampling distribution with higher density on areas that contribute more to the expectation. Despite its name, importance sampling is not a true sampling method; it's an approximation method and does not involve a sampling process.

Importance sampling introduces two distributions: the target distribution \(p(x)\) and the proposal distribution \(q(x)\). The target distribution describes the true underlying distribution of the data, whereas the proposal distribution is the new distribution we will sample from. In importance sampling, we want to control how often we sample certain values. As stated, we usually want \(q(x)\) to have high density on areas that contribute more to the expectation. What does this exactly mean?

In Figure 1, we can see that \(p(x)\) will have trouble sampling from the right side of \(f(x)\), which is where all the action is happening. Meanwhile, \(q(x)\) will do a pretty good job at sampling from the important areas (where the action is happening); hence, importance sampling.

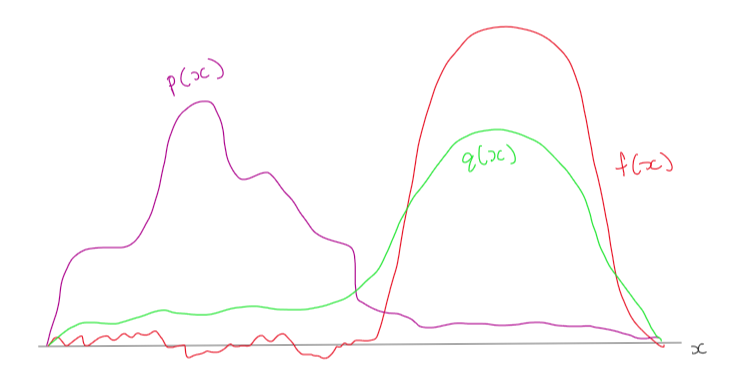
Now it’s important to note that, in the long run, it really doesn’t matter which distribution we use, because Monte Carlo estimates are unbiased. However, it is also important to note that, if we sample from q(x) instead of p(x), our estimate will have a smaller variance, resulting in higher accuracy.

$$\sigma^2(I_n) = \frac{1}{n} \sigma^2(f(x)\frac{p(x)}{q(x)})$$

As an aside, in some applications, importance sampling is used to solve the problem of sampling from an intractable density. In this case, typically q(x) is chosen to be as close to the true (but intractable) distribution p(x).

Now that we have the big idea, how do we do the derivation? It’s actually really simple! We’ll start with the expectation, then multiplying by q(x) q(x) and finally applying Monte Carlo approximations,

$$ \begin{align*} E(f(x)) &= \int f(x)p(x)dx\\ &= \int f(x)\frac{p(x)}{q(x)}q(x)dx\\ &\approx \frac{1}{n} \sum_{i=1}^n f(x_i)\frac{p(x_i)}{q(x_i)}\\ &= \frac{1}{n}\sum_{i=1}^n f(x_i)w(x_i) \end{align*} $$

where

$$w(x)=\frac{p(x)}{q(x)}, \hspace{1cm} x_i \sim q(x)$$